TRANSCENDANTS (NOMBRES)

TRANSCENDANTS (NOMBRES)

Si la notion de nombre irrationnel remonte aux Grecs, l’idée de nombre transcendant n’a pu se dégager qu’après la création de notations algébriques assez développées pour que le concept de polynôme de degré quelconque puisse être clairement formulé; aussi est-ce seulement au XVII^e siècle que l’on commence à faire la distinction entre les nombres algébriques , tels 連3/2 ou cos ( 神/n ) pour n entier, qui sont racines de polynômes à coefficients entiers , les autres nombres réels étant qualifiés de transcendants . L’existence de nombres transcendants n’a été prouvée qu’au XIX^e siècle; s’il est facile de construire des nombres transcendants, la question de savoir si un nombre donné est ou non transcendant est généralement un problème fort difficile. L’exemple le plus célèbre est celui du nombre 神, dont la transcendance n’a été démontrée qu’en 1882; ce résultat prouvait définitivement l’impossibilité de la «quadrature du cercle», c’est-à-dire le problème, posé depuis les Grecs, de la construction géométrique «par la règle et le compas» d’une longueur égale à la circonférence de diamètre unité; il est facile, en effet, de montrer qu’une telle construction ne peut jamais donner que des longueurs dont la mesure est un nombre algébrique (et même un nombre algébrique d’un type très particulier).

L’existence des nombres transcendants

Il est commode d’étendre la définition des nombres algébriques aux nombres complexes, et d’appeler encore nombre transcendant un nombre complexe non algébrique. J. Liouville a établi, en 1844, l’existence des nombres transcendants par une construction fondée sur la propriété, découverte par lui, de «mauvaise approximation» des nombres irrationnels algébriques par les nombres rationnels (cf. approximations DIOPHANTIENNES). En 1873, G. Cantor déduisit l’existence des nombres transcendants de son théorème prouvant que l’ensemble de tous les nombres réels est non dénombrable: il suffit, en effet, de prouver que l’ensemble A de tous les nombres algébriques est dénombrable. Pour cela, associons à chaque polynôme à coefficients entiers:

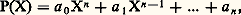sa hauteur :

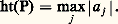Comme un polynôme n’a qu’un nombre fini de racines, l’ensemble A^N des nombres algébriques qui sont racines de polynômes à coefficients entiers de degré 諒 N et de hauteur 諒 N est un ensemble fini ; comme A est réunion des A^N, pour N = 1, 2, ... l’ensemble A est dénombrable.

L’ensemble des nombres transcendants n’est donc pas dénombrable; en termes imagés, on peut dire qu’un nombre pris au hasard (par exemple en se donnant au hasard son développement décimal illimité) n’a «aucune chance» d’être algébrique.

Valeurs transcendantes de fonctions entières

Le premier résultat profond sur les nombres transcendants fut obtenu par C. Hermite en 1872: par une méthode très originale reposant sur l’approximation de la fonction exponentielle e ^z par des fonctions rationnelles, il put montrer que le nombre e est transcendant, et c’est par une extension de la méthode d’Hermite que Ferdinand von Lindemann, en 1882, prouva que 神 est aussi transcendant. De nouveaux résultats de cette nature n’apparurent qu’après 1929; ils concernent, comme les précédents, des nombres qui sont des valeurs prises par certaines fonctions entières ou méromorphes (ou leurs fonctions inverses) pour des valeurs algébriques de la variable; les méthodes, développées à partir d’idées de C. L. Siegel et de A. Gelfond, raffinées par T. Schneider et récemment par A. Baker, utilisent, comme celle d’Hermite, des propriétés des fonctions entières d’une variable complexe. Aucune méthode n’a encore été trouvée pour des nombres qui ne sont pas donnés de cette manière, par exemple la constante d’Euler:

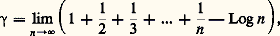dont on ne sait même pas si elle est irrationnelle (cf. chap. 2 de l’article calculs ASYMPTOTIQUES).

Les théorèmes d’Hermite et de Lindemann sont des cas particuliers du résultat suivant.

Théorème I . Un nombre complexe 見 0 ne peut être tel que 見 et e size=1^見 soient tous deux algébriques.

En effet, ce théorème entraîne, en faisant 見 = 1, que e est transcendant et, en faisant 見 = i 神, que 神 est transcendant.

La méthode de Siegel-Gelfond-Schneider déduit le théorème I d’un théorème plus général concernant les valeurs de deux fonctions entières liées par des équations différentielles algébriques :

Théorème II . Soit f et g deux fonctions entières d’ordre fini 福, c’est-à-dire vérifiant des majorations,

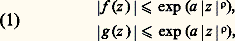pour tout z 捻 C. On suppose que:

1^o Les fonctions f et g sont algébriquement indépendantes, c’est-à-dire qu’il n’existe aucun polynôme P(X, Y) non nul à coefficients complexes tel que P(f (z ), g (z )) 令 0.

2^o On a des relations différentielles:

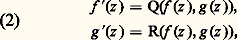où Q et R sont des polynômes à coefficients dans un corps de nombres algébriques K de degré fini d sur le corps des rationnels Q.

Supposons alors qu’il y ait m nombres complexes distincts w ¹, ..., w ^m tels que les 2m nombres f (w ^j ) et g (w ^j ) appartiennent à K. Cela n’est possible que si m 諒 10 福d .

Pour en tirer le théorème I, on prend f (z ) = z et g (z ) = e ^z , qui vérifient les conditions (1) et (2); si 見 et e size=1^見 étaient algébriques, ils appartiendraient à un même corps de nombres K de degré fini; mais alors tous les nombres n 見 et e ⁿ size=1^見 appartiendraient aussi à K pour tout entier n , ce qui contredit le théorème II.

Si 廓 est un nombre algébrique irrationnel, les fonctions e ^t et e size=1^廓t vérifient les conditions du théorème II en prenant pour K un corps contenant 廓. On en déduit le théorème de Gelfond-Schneider :

Théorème III . Si 見 est un nombre algébrique autre que 0 et 1 et 廓 un nombre algébrique irrationnel, le nombre 見廓 = exp ( 廓 Log 見), avec une détermination quelconque du logarithme, est transcendant.

En effet, dans le cas contraire, les valeurs de e ^t et e size=1^廓t pour tous les nombres n Log 見, avec n entier quelconque, appartiendraient à un corps K contenant 見 et 見 size=1^廓, contrairement au théorème II.

Par exemple, le nombre 2 連2 et le nombre e size=1^神, qui est une détermination de (face=F0019 漣 1)^-i , sont transcendants.

L’idée de la démonstration du théorème II est de former une suite (F^s (z )) de fonctions entières d’ordre 福, où l’indice s prendra des valeurs entières arbitrairement grandes , qui possèdent les propriétés suivantes, où C¹, C², ... sont des constantes indépendantes de s ,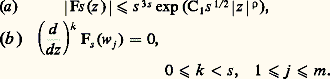

(c ) Il existe un w ^j , par exemple w ¹, tel que:

et tel que: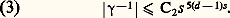

On remarque alors que la fonction:

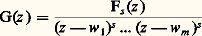est une fonction entière en vertu de (b ) qui, pour |z | 諒 R, où R est assez grand, vérifie, en vertu de (a ) et du principe du maximum, l’inégalité:

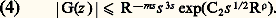D’autre part, on a:

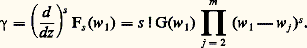On prend R = s ^1/(2 size=1^福), et on déduit de (4) la majoration:

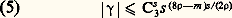et, en comparant avec la minoration de | 塚| donnée par (3), on obtient aisément m 諒 10 福d .

Tout revient donc à satisfaire aux conditions (a ), (b ) et (c ). On se donne un entier r arbitrairement grand divisible par 2m et on pose n = r ²/(2 m ). On considère la fonction: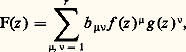

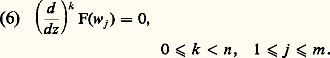où l’on détermine les coefficients b size=1^猪益 dans K tels que:

C’est un système de mn équations linéaires à r ² = 2 mn inconnues b size=1^猪益, dont les coefficients sont par hypothèse dans K, en vertu des relations (2) et de l’hypothèse sur les f (w ^j ) et g (w ^j ). On montre par des majorations élémentaires que l’on peut prendre pour solutions b size=1^猪益 de ce système des entiers de K non tous nuls tels que:

L’hypothèse que f et g sont algébriquement indépendantes implique alors que F n’est pas identiquement nulle. Il y a donc un plus petit entier s tel que F = F^s vérifie (b ) et que: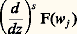

ne soit pas nul pour un j au moins; en vertu de (6), on a nécessairement s 閭 n . On prouve élémentairement qu’il y a un nombre rationnel c 諒 C^{s 5} tel que c 塚 soit un entier algébrique de K et que c 塚 et tous ses conjugués soient majorés par C⁶s ^5s en valeur absolue. Pour la norme de c 塚, qui est un entier rationnel non nul, on a alors les inégalités:

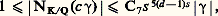ce qui donne (3); quant à la majoration (a ) de F^s , elle se déduit aisément des majorations de f et g et de (7).

A. Baker a généralisé les théorèmes I et III; désignons par L l’ensemble des nombres complexes z tels que e ^z soit un nombre algébrique; c’est évidemment un sous-espace vectoriel de C sur le corps Q des nombres rationnels. Alors, on a les résultats suivants de Baker:

Théorème IV . (a ) Si z ¹, ..., z ⁿ sont des éléments de L linéairement indépendants sur Q, ils sont aussi linéairement indépendants sur le corps de tous les nombres algébriques, autrement dit il ne peut exister de relation:

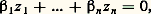avec des coefficients algébriques 廓¹, ..., 廓ⁿ non tous nuls.

(b ) Si z ¹, ..., z ⁿ sont des éléments de L, il ne peut exister de relation:

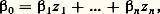où 廓⁰, 廓¹, ..., 廓ⁿ sont des nombres algébriques et où l’on a 廓⁰ 0.

On déduit aussitôt du théorème IV que, si 廓¹, ..., 廓ⁿ sont des nombres algébriques tels que 1, 廓¹, ..., 廓ⁿ soient linéairement indépendants sur Q, alors le nombre:

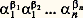est transcendant pour tous les 見^j algébriques différents de 0 et de 1. De même, si 見¹, ..., 見ⁿ , 廓⁰, 廓¹, ..., 廓ⁿ sont des nombres algébriques non nuls, le nombre:

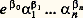est transcendant. On déduit aussi par exemple du théorème IV que 神 + Log 見 est transcendant pour tout nombre algébrique 見 0.

La méthode de démonstration du théorème IV est une extension de celle du théorème II, mais utilisant une technique plus subtile; pour (b ), par exemple, on raisonne par l’absurde en supposant l’existence d’une relation: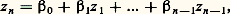

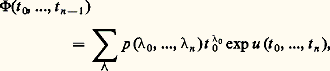et on considère la fonction entière de n variables complexes t ⁰, t ¹, ..., t ^{n -1}:

où: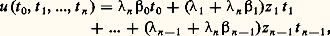

lesⁿ étant des entiers tels que 0 諒^j 諒 c ¹. On impose aux p () d’être entiers et choisis de sorte que 淋 et toutes ses dérivées partielles jusqu’à un ordre c ² s’annulent lorsqu’on y fait t ¹ = t ² = ... = t ^{n -1} = w et que w est un entier tel que 0 諒 w 諒 c ³. Par un choix convenable des constantes c ¹, c ², c ³ et l’emploi de majorations tirées de la théorie des fonctions holomorphes, on aboutit à une contradiction.

Indépendance algébrique de nombres transcendants

La transcendance d’un nombre 見 signifie qu’il n’est pas racine d’un polynôme à coefficients entiers. Plus généralement, n nombres complexes 見¹, 見², ..., 見ⁿ sont dits algébriquement indépendants s’il n’existe aucun polynôme non nul P(T¹, ..., Tⁿ ) à n indéterminées et à coefficients entiers tel que P( 見¹, ..., 見ⁿ ), = 0, ce qui implique bien entendu que 見¹, ..., 見ⁿ sont transcendants. On n’a que peu de résultats sur cette question; par exemple, on ignore si e et 神 sont algébriquement indépendants. On conjecture que, sous les conditions (a ) du théorème IV, les z ^j sont algébriquement indépendants.

Les résultats positifs les plus intéressants sont les suivants:

Théorème V (Lindemann). Si 見¹, ..., 見ⁿ sont des nombres algébriques linéairement indépendants sur Q, les nombres e size=1^見1, ..., e size=1^見n sont algébriquement indépendants.

Théorème VI (Siegel) . Si J ⁰ est la fonction de Bessel d’indice 0, alors les nombres J⁰( 見) et J ⁰( 見) sont algébriquement indépendants pour tout nombre algébrique 見 0.

Une même méthode, due à Siegel, permet de démontrer ces deux résultats. Elle applique une idée analogue à celle de la démonstration du théorème II, utilisant le fait que les fonctions e ^az et J⁰(z ) vérifient une équation différentielle linéaire homogène et des majorations tirées de la théorie des fonctions analytiques; mais les détails de la démonstration sont beaucoup plus délicats et compliqués.

Encyclopédie Universelle. 2012.